|
|
|
|
Dave W.
Info Junkie
USA
26020 Posts |
 Posted - 07/17/2009 : 07:49:55
|
What is the explanation for this:
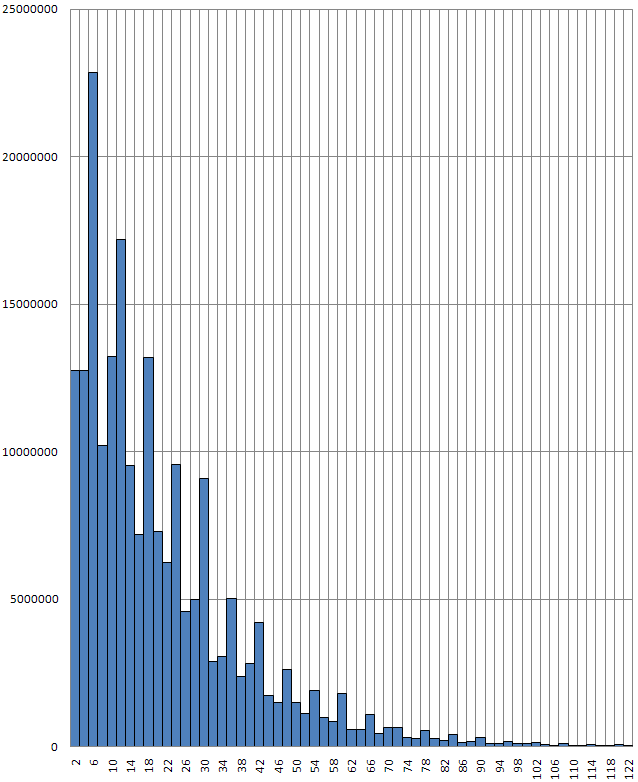
The above is a histogram of the differences between neighboring primes (between 3 and 4,294,967,291 inclusive). Why are differences that are multiples of six overrepresented? Multiples of ten also appear to be overrepresented, just not as obviously as multiples of six.
The last time I did any prime hunting was about 20 years ago, using highly optimized assembly code (with a brute-force algorithm) it took my poor computer several weeks to get through all 2-billion-and-change candidate numbers representable in 32 bits or less.
This time, on my two-year-old home machine, with a Java routine I threw together in under an hour, it found all 203,280,221 primes in about 10 hours, 15 minutes. Home computers have come a long way.
The full list of difference data can be found here. The multiples-of-six/ten pattern appears to hold all the way through differences of 282 (but the largest difference in the first 32-bits' worth of primes is only 336 (twice), so we're talking about outliers, anyway.
|
- Dave W. (Private Msg, EMail)
Evidently, I rock!
Why not question something for a change?
Visit Dave's Psoriasis Info, too. |
|
|
Simon
SFN Regular
USA
1992 Posts |
Posted - 07/17/2009 : 07:56:17 [Permalink]
|
God wanted it that way.
(The previous message was brought to you by the Texas Board of Edumucation)
Seriously though, no idea. |
Look again at that dot. That's here. That's home. That's us. On it everyone you love, everyone you know, everyone you ever heard of, every human being who ever was, lived out their lives. The aggregate of our joy and suffering, thousands of confident religions, ideologies, and economic doctrines, every hunter and forager, every hero and coward, every creator and destroyer of civilization, every king and peasant, every young couple in love, every mother and father, hopeful child, inventor and explorer, every teacher of morals, every corrupt politician, every "superstar," every "supreme leader," every saint and sinner in the history of our species lived there – on a mote of dust suspended in a sunbeam.
Carl Sagan - 1996 |
 |
|
|
Ricky
SFN Die Hard
USA
4907 Posts |
|
|
Dude
SFN Die Hard
USA
6891 Posts |
Posted - 07/18/2009 : 20:12:34 [Permalink]
|
What is this "math" thing you speak of?
....
Mathematics requires effort to learn, therefore I tend to avoid it.
Its a character flaw, I know.
|
Ignorance is preferable to error; and he is less remote from the truth who believes nothing, than he who believes what is wrong.
-- Thomas Jefferson
"god :: the last refuge of a man with no answers and no argument." - G. Carlin
Hope, n.
The handmaiden of desperation; the opiate of despair; the illegible signpost on the road to perdition. ~~ da filth |
|
|
|
|
Dave W.
Info Junkie
USA
26020 Posts |
Posted - 07/18/2009 : 21:46:30 [Permalink]
|
Originally posted by Ricky
The same explanation goes for multiples of 10 = 2 * 5. |
And then for 12, 14, 15, etc?
So is the relative equality of the 2- and 4-gap counts due to the fact that every other multiple of two is a multiple of four?
Wait a minute... What the chart is really saying is that for any prime, p, it is nearly twice as likely that both p+2 and p+4 are not prime, than it is that either p+2 or p+4 are prime.
Is there an equation that gives the odds that the sum of a prime and some even integer is also prime?
I've gotta calculate more primes... |
- Dave W. (Private Msg, EMail)
Evidently, I rock!
Why not question something for a change?
Visit Dave's Psoriasis Info, too. |
|
|
|
Ricky
SFN Die Hard
USA
4907 Posts |
Posted - 07/19/2009 : 00:05:10 [Permalink]
|
| So is the relative equality of the 2- and 4-gap counts due to the fact that every other multiple of two is a multiple of four? |
I don't think that's it. If I start with a prime number p, and I add 2 to it, and then add 2 again, one of those numbers has to be divisible by 3. I would imagine this is what is causing those results to be approximately equal.
| for any prime, p, it is nearly twice as likely that both p+2 and p+4 are not prime, than it is that either p+2 or p+4 are prime. |
Where do you get this from? The histogram tells you no information about how many results are coming from the same prime p, or two different primes p and q.
Is there an equation that gives the odds that the sum of a prime and some even integer is also prime?
|
To my knowledge, no. Most results in prime distribution (the famous ones, anyways) are about the asymptotic behavior of primes (Bertrand's postulate, Euler's harmonic series of primes). |
Why continue? Because we must. Because we have the call. Because it is nobler to fight for rationality without winning than to give up in the face of continued defeats. Because whatever true progress humanity makes is through the rationality of the occasional individual and because any one individual we may win for the cause may do more for humanity than a hundred thousand who hug their superstitions to their breast.
- Isaac Asimov |
|
|
|
Dave W.
Info Junkie
USA
26020 Posts |
Posted - 07/19/2009 : 01:24:40 [Permalink]
|
Originally posted by Ricky
| So is the relative equality of the 2- and 4-gap counts due to the fact that every other multiple of two is a multiple of four? |
I don't think that's it. If I start with a prime number p, and I add 2 to it, and then add 2 again, one of those numbers has to be divisible by 3. I would imagine this is what is causing those results to be approximately equal. |
Yes, but the same could be said about adding 8 to a prime (and then 8 again), but there's a big difference in the number of 8-gaps and the number of 16-gaps.| for any prime, p, it is nearly twice as likely that both p+2 and p+4 are not prime, than it is that either p+2 or p+4 are prime. |
Where do you get this from? The histogram tells you no information about how many results are coming from the same prime p, or two different primes p and q. |
All of the data that went into the histogram compares every prime to its nearest larger prime. So we can say with certainty that given a randomly selected prime p greater than 2 and less than 4,294,967,291 that there's an 11.2416% chance that its next-largest neighboring prime (NLNP) will be p+6, but only a 6.2670% chance that its NLNP will be p+2 and a 6.2674% chance that its NLNP will be p+4 (and, of course, a 76.2241% that its NLNP will be p+8 or greater).
By the way, I've revised my Java code to hunt for primes up to 1.6 trillion (or so), and given what I write below, I suspect that the odds will change for the worse.| Is there an equation that gives the odds that the sum of a prime and some even integer is also prime? |
To my knowledge, no. Most results in prime distribution (the famous ones, anyways) are about the asymptotic behavior of primes (Bertrand's postulate, Euler's harmonic series of primes). |
Thinking about it, as p heads toward infinity, there are more and more possible divisors for any given odd integer, and so the high-p primes should favor larger NLNPs over time, thus flattening the distribution curve, yes? With an infinite number of primes, the histogram ought to be flat, otherwise there'd be some pattern of distribution that should have been discovered by some math wiz already, right? I mean, I don't imagine that I'm breaking any new ground, here. |
- Dave W. (Private Msg, EMail)
Evidently, I rock!
Why not question something for a change?
Visit Dave's Psoriasis Info, too. |
|
|
|
Zebra
Skeptic Friend
USA
354 Posts |
Posted - 07/20/2009 : 21:00:46 [Permalink]
|
Here's the little bit I can add, thanks to the internet.
The difference between 2 consecutive primes numbers is called the Prime gap, and as you can see at the top of the linked page, there are a bunch of 6's early on.
The unevenness in the distribution does disappear as you find more primes (makes sense, but I'm stating it authoratively because several sources suggest it's so).
See here (a graph linked at the page linked to the sequence at the top of the Wikipedia page - apparently of the prime gaps - I'm not sure how many primes/gaps this one includes, but it's alot ).
See also this 2005 paper, esp the graphs on pages 2 & 8. The authors show an oscillation of short periodicity in the prime gap histogram for the first million primes.
|
I think, you know, freedom means freedom for everyone* -Dick Cheney
*some restrictions may apply |
|
|
|
Dave W.
Info Junkie
USA
26020 Posts |
Posted - 07/21/2009 : 12:56:40 [Permalink]
|
Thanks for that 2005 paper, Zebra. I think perhaps it held one of the key ingredients I was missing: that all primes over 3 are of the form 6n±1. (I knew this in the back of my head somewhere, it just wasn't connecting.) Which suggests something I hadn't thought of before: when searching for primes we can skip testing every third odd number over 3 (since we know it'll be a 6n+3 number), and by doing so speed up testing by nearly a third. So starting with 5, we can add 2 and test (7), add four and test (11), add 2 and test (13), add 4 and test (17), etc.. Just +2, +4, +2, +4 and on and on.
Eventually, we run into 25. We know that's a multiple of 5, and so doesn't need to be tested, either. We can add skipping multiples of 5 by making the pattern more complex. Starting with seven, we can go +4, +2, +4, +2, +4, +6, +2, +6, and that gets us to 37, after which we repeat the pattern. So we're down to testing only 8 numbers out of every 30, so instead of testing all odd numbers, or even 2/3rds of the odd numbers, we'd only be testing 53% of the odd numbers.
And so on. We can remove multiples of 7 with a pattern that cycles over 210 numbers, and we can remove multiples of 11 with a pattern that cycles over 2,310 numbers. And on an on, however much memory we want to devote to the pattern. I think, however, we'd quickly run into diminishing returns in terms of reducing the percentage of numbers which still need to be checked. And while the size of the pattern for removing multiples of 2 and 3 was 2, and the size for removing 2, 3 and 5 was 8, if we hit a pattern size that isn't a power of two, then we will start to make the algorithm inefficient again (since counting through the pattern modulo some-power-of-2 can be reduced to a single bitwise AND function, whereas non-powers-of-2 require either an actual division or an if/then construct). |
- Dave W. (Private Msg, EMail)
Evidently, I rock!
Why not question something for a change?
Visit Dave's Psoriasis Info, too. |
|
|
|
Zebra
Skeptic Friend
USA
354 Posts |
Posted - 07/22/2009 : 21:18:02 [Permalink]
|
Originally posted by Dave W.
Thanks for that 2005 paper, Zebra. I think perhaps it held one of the key ingredients I was missing: that all primes over 3 are of the form 6n±1. (I knew this in the back of my head somewhere, it just wasn't connecting.) Which suggests something I hadn't thought of before: when searching for primes we can skip testing every third odd number over 3 (since we know it'll be a 6n+3 number), and by doing so speed up testing by nearly a third. So starting with 5, we can add 2 and test (7), add four and test (11), add 2 and test (13), add 4 and test (17), etc.. Just +2, +4, +2, +4 and on and on.
Eventually, we run into 25. We know that's a multiple of 5, and so doesn't need to be tested, either. We can add skipping multiples of 5 by making the pattern more complex. Starting with seven, we can go +4, +2, +4, +2, +4, +6, +2, +6, and that gets us to 37, after which we repeat the pattern. So we're down to testing only 8 numbers out of every 30, so instead of testing all odd numbers, or even 2/3rds of the odd numbers, we'd only be testing 53% of the odd numbers.
And so on. We can remove multiples of 7 with a pattern that cycles over 210 numbers, and we can remove multiples of 11 with a pattern that cycles over 2,310 numbers. And on an on, however much memory we want to devote to the pattern. I think, however, we'd quickly run into diminishing returns in terms of reducing the percentage of numbers which still need to be checked. And while the size of the pattern for removing multiples of 2 and 3 was 2, and the size for removing 2, 3 and 5 was 8, if we hit a pattern size that isn't a power of two, then we will start to make the algorithm inefficient again (since counting through the pattern modulo some-power-of-2 can be reduced to a single bitwise AND function, whereas non-powers-of-2 require either an actual division or an if/then construct).
|
Well, heck! When you put it that way, who needs a computer to find primes at all? 
Edited to add emphasis
|
I think, you know, freedom means freedom for everyone* -Dick Cheney
*some restrictions may apply |
| Edited by - Zebra on 07/22/2009 21:19:15 |
|
|
|
 |
|
|
|
Calling all math geeks
